carstenj

Matematik er smukt II - Eulers identitet

2014-02-18

Via BBC’s website fandt min kone artiklen The experience of mathematical beauty and its neural correlates.

Jeg forbinder ord som ro, glæde, smukt og orden med mine egne matematik oplevelser. Nu har en række forskere vist, at de områder i hjernen som aktiveres, når man ser på en “smuk” ligning, er de samme områder i hjernen som aktiveres, hvis man eksempelvis ser på et smukt maleri eller lytter til smuk musik.

I forsøget blev en gruppe matematikere vist en række formler og bedt om at score dem fra grim til smuk.

Den ligning som i gennemsnit scorer højest som værende den smukkeste ligning er Eulers identitet:

Ligningen ser utrolig simpel og elegant ud, og det fantastiske er, at man i en og samme ligning forbinder fem centrale matematiske konstanter og tre regnearter.

Lad os starte med konstanterne:

• $1$ er det multiplikative enhedselement, dvs for alle tal $x$ gælder $x1=1x=x$
• $0$ er det additive enhedselement, dvs for alle tal $x$ gælder $x+0=0+x=x$
• $e$ er basen i den naturlige logaritme som anvendes i mange former for matematisk analyse, $e = 2.718281828\ldots$
• $\pi$ kendes fra både geometri og trigometri, $\pi = 3.14159265\ldots$
• $i$ er det komplekse tal som opfylder $i^2 = -1$

Og herefter regnearterne:

• Addition
• Multiplikation
• Eksponentiation

Det er ikke svært at bevise Eulers identitet, men lad os hellere forsøge at opbygge en intuitiv forståelse for korrektheden af ligningen. Eksponentialfunktionen kan f.eks. karakteriseret ved en uendelig sum:

eller som en grænseværdi

Denne ligning gælder naturligvis også, hvis man vælger $x=i\pi$,

Ved brug af en computer, er det nemt at udregne det komplekse tal $\left(1 + \frac{i\pi}{n}\right)^n$ for et vilkårligt $n$. Hvis man f.eks sætter $n=4$, kan man udregne disse fire komplekse tal

Komplekse tal er kendetegnet ved at have en real og en imaginær del, hvorfor vi kan skrive $z_k$ som $R_k + i I_k$ for passende valg af $R_k$ og $I_k$. Hvis man nu afbilder punkterne $(R_k, I_k)$ i den komplekse plan og forbinder dem med en ret linje ser vi både hvor de enkelte punkter ligger men mere vigtigt får vi placeres endepunktet $\left(1 + \frac{i\pi}{4} \right)^4$. Bemærk at alle graferne starter i punktet $(1,0)$, da $\lim_{n\rightarrow 0} \left(1+ \frac{x}{n}\right)^n = 0$.

Nedenfor findes et Python program som udregner sådanne tal for $n=1,2,3,4,5,10,20,50,1000$ og dernæst laver en graf med tallene.

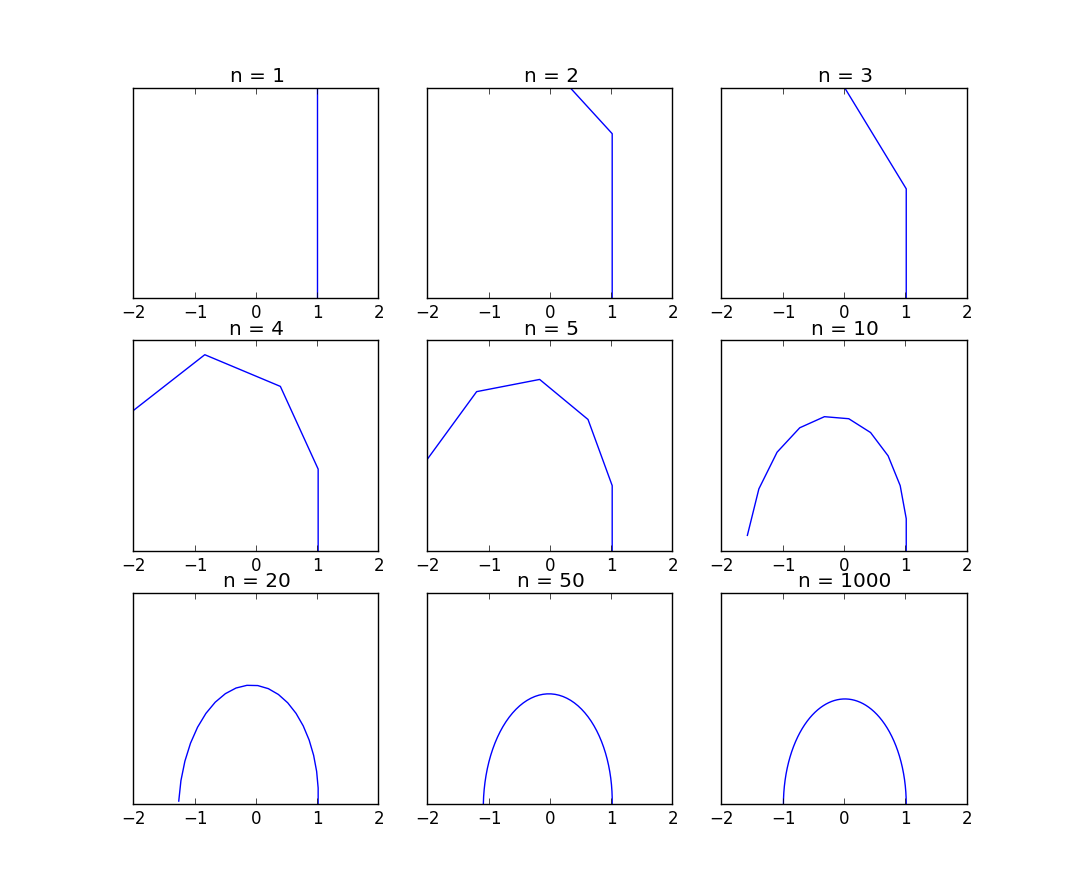
For $n=1000$ i grafen nederst i højre hjørne ser vi, hvordan rækken konvergerer mod $-1$ eller med andre ord

Ovenstående eksempel findes i en udvidet version i bogen “Dr. Euler’s Fabulous Formula” af Paul Nahin, udgivet i 2006.

Den formel, som fik den dårligste score, var Srinivasa Ramanujans formel for den reciprokke værdi af $\pi$ udtrykt som en uendelige sum:

Og det er måske ikke så svært at forstå :-)

Jeg er Python nybegynder, så lad mig endelig vide, hvis programmet med fordel kan skrives anderledes.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import re
import matplotlib.pyplot as plt
import math
import cmath

plt.close('all')

n = [1, 2, 3, 4, 5, 10, 20, 50, 1000]
l = 1

for N in n:
    x = [1]
    y = [0]  
    c = 1 + (1j * math.pi) / N
    z = [c]
    for loop in xrange(1, N):
        z.append(z[loop - 1] * c)
    for loop in xrange(1, N + 1):
        x.append(z[loop - 1].real)
        y.append(z[loop - 1].imag)
   
    sp = plt.subplot(3, 3, l)
    sp.plot(x, y)
    sp.set_yticks([]) 
    sp.set_ylim([0, 2])
    sp.set_xlim([-2, 2])
    sp.xaxis.set_ticks(np.arange(-2, 3, 1))
    plt.title("n = " + str(N))
    l = l + 1

plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=1.0)     
plt.show()    

</script>

---

Please create issues at the Github repo Twitter.

Edit page on GitHub. Please help me to improve the blog by fixing mistakes on GitHub. This link will take you directly to this page in our GitHub repository.

There are more posts on the front page.

Content of this blog by Carsten Jørgensen is licensed under a Creative Commons Attribution 4.0 International License.